Background
It’s the most wonderful time of the year: Christmas. Every year, kids (and some adults) eagerly wait for Santa to deliver their presents. As you watch the Santa Trackers, you’re probably wondering if Dasher or Rudolph could fly a little quicker so that the presents get delivered sooner.
This version of Santa’s sleigh, named the Jingle Jet, is designed and drawn by Mikael Sedlacek. It’s equipped with 2 jet turbo engines; therefore, this sleigh does not require the services of Santa’s 10 reindeer. The Jingle Jet is designed with an aerodynamic body so that it can glide through the sky.
Technical Length:
- Length: 17.55 ft
- Width (Parked Config): 11.93 ft
- Height: 4.92 ft
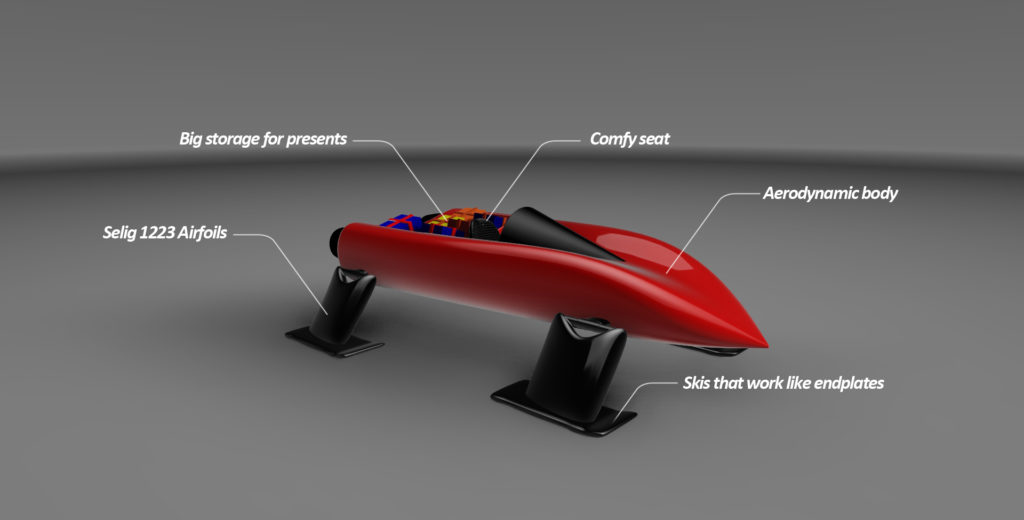
Breakdown of Santa’s Jet Turbo sleigh [1]
Run Conditions
The simulation was solved with a flow velocity of 150 mph at a altitude of 5,000 ft.
Run Stats
- Vehicle CAD file [2] was prepped and processed via Beta CAE’s ANSA v18.10.
- Meshed with snappyHexMesh (part of OpenFOAM)
- Vehicle was meshed and solved on 48 cores
- Mesh Size: 19.7 million cells
- Solved using TotalSim’s version of OpenFOAM (simplec solver)
- Jets off, vehicle is in glide mode…
Analysis
Note: Geometry file was drawn by an enthusiast and the numbers/plots below may not accurately depict the vehicle.
Aerodynamic Forces
The simulation reported that the Jingle Jet generated 560.6 lb of Drag and 802 lb of Lift. Non-dimensionalizing the forces yields a CD of 0.35 and 0.48 for CL. Just to compare, a typical car has a Cd of ~0.30 and a model rocket has a Cd of 0.75 [3].
The Aerodynamic Efficiency, which is the ratio of lift to drag (L/D), is 1.36. Typically, a higher L/D is favorable and often a key metric for aircraft designers. A higher L/D is typically associated with longer endurance or a smaller glide slope angle. Typical L/D ratios include 4 for a helicopter, 15-20 for commercial aircraft, and 2.5 for a gliding wingsuit [4].
Cp Plots
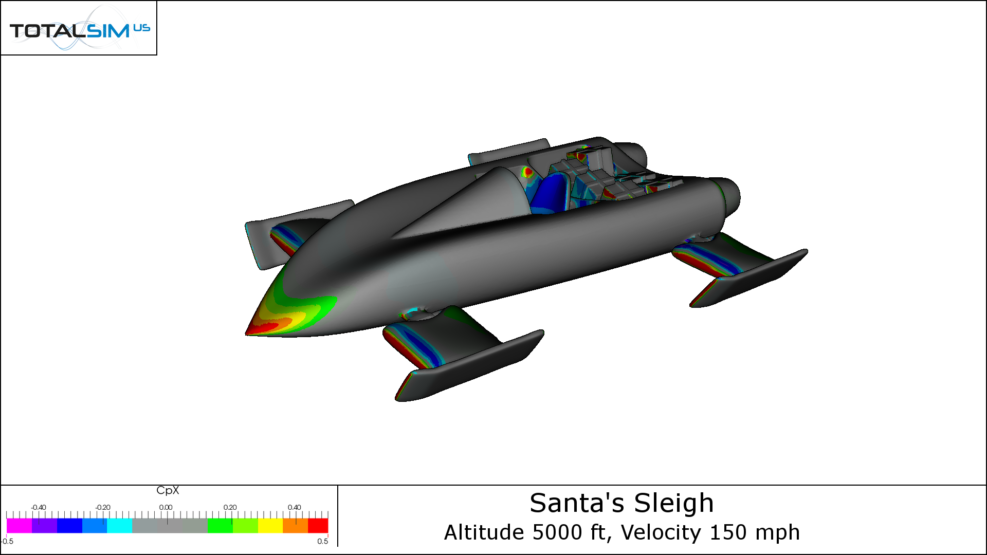
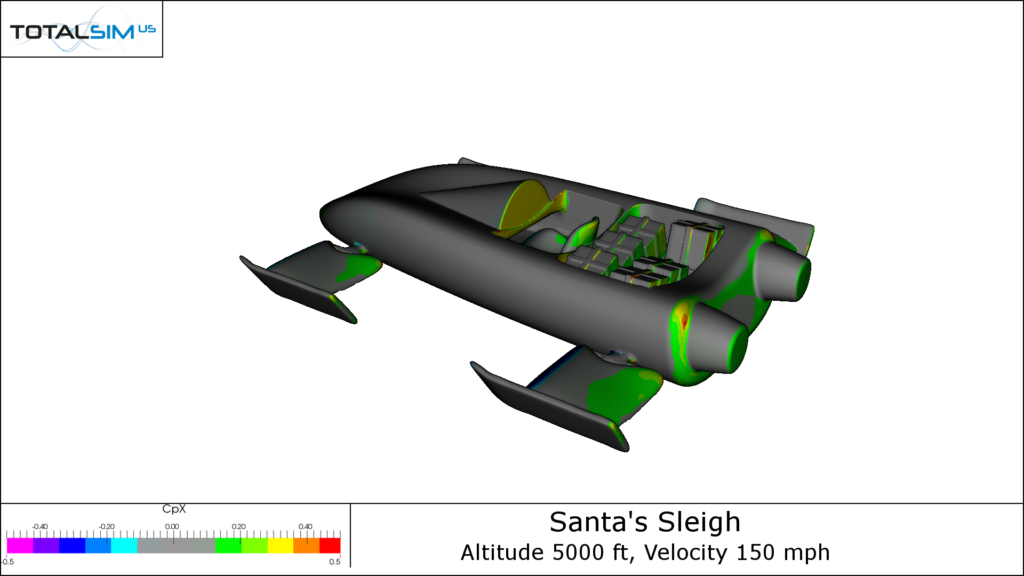
By looking at the pressure surface plots, we can understand how these forces are being created. Warm colors shows regions of high pressure and cool colors show regions of low pressure. By isolating pressure in the x direction (longitudinally) and the z-direction (vertically), we would be able to see the influences of drag and lift on the Jingle Jet.
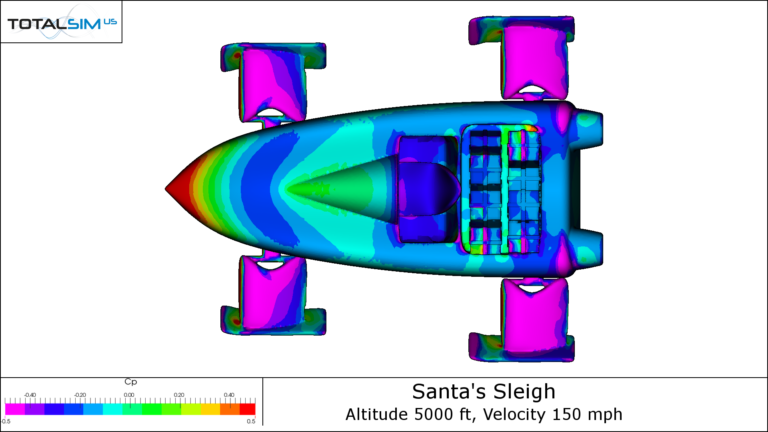
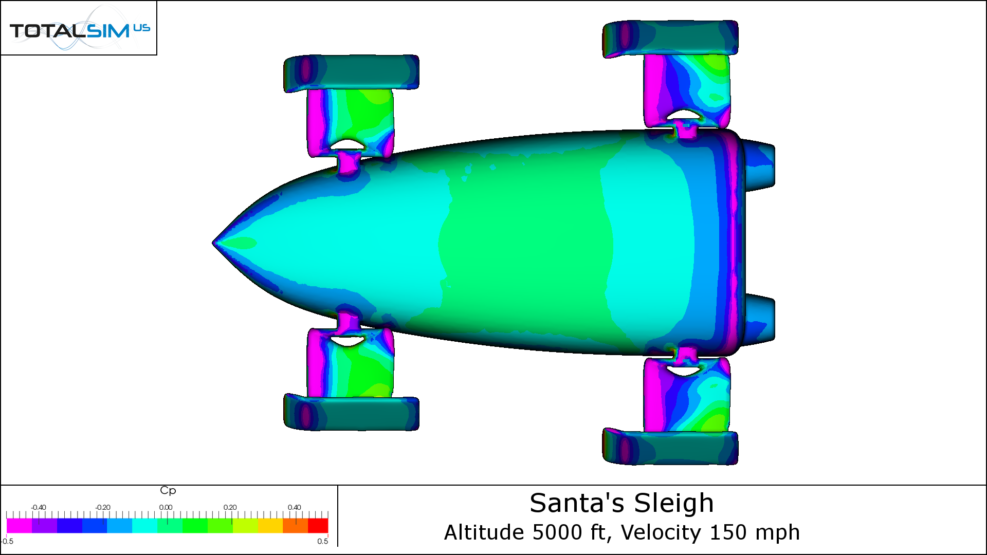
CpX Plots
As expected, the Jingle Jet’s sleeker aerodynamic body shows little in the way of Drag production. Stagnation pressure drag is seen on the nose and at the Leading edges of the landing gear arms. The gear arms also show regions of thrust where the flow accelerates over the upper surface which is expected for a highly cambered airfoil like the Selig 1223. Base drag can be seen on the rear face of the Jingle Jet as well as on the dashboard. Interestingly, the low pressure region created by the backward facing surfaces of the Dashboard is imprinted on the seat making it look as though the seat is producing thrust
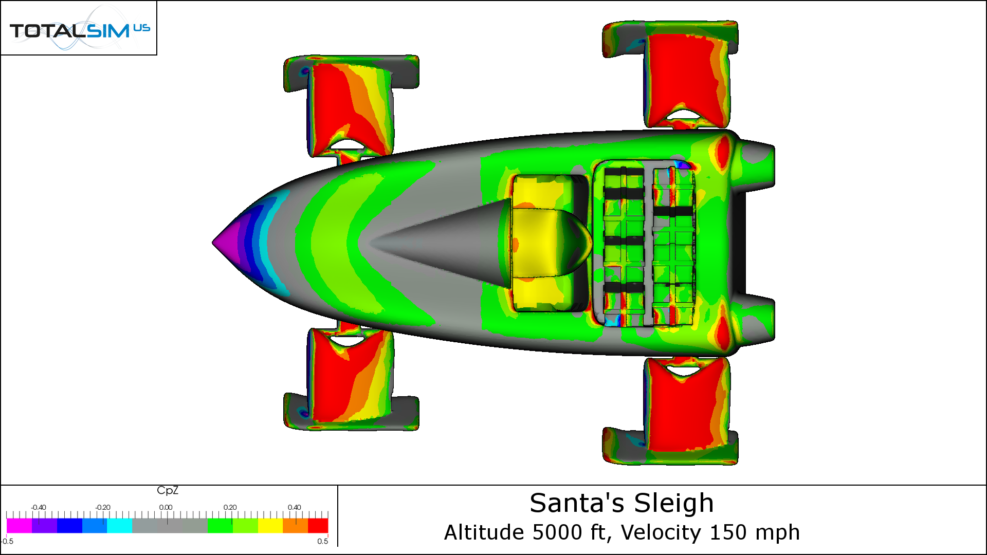
CpZ Plots
The upper surface of the Jingle Jet is pure mostly lift production except for the region around the nose. This is mostly because the nose slopes downward and the stagnation pressure forces this region to push down on the vehicle. The underbody seems to be producing a fair amount of downforce. Part of this stems from the flow accelerating around to the lower body. The low pressure behind the rear of the vehicle appears to be responsible for the downforce generated near the back.
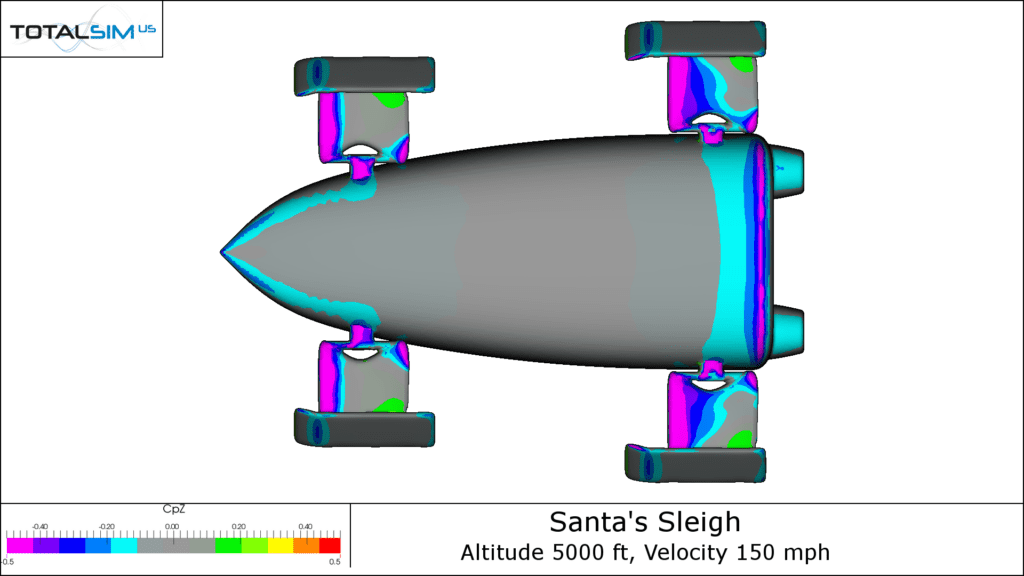
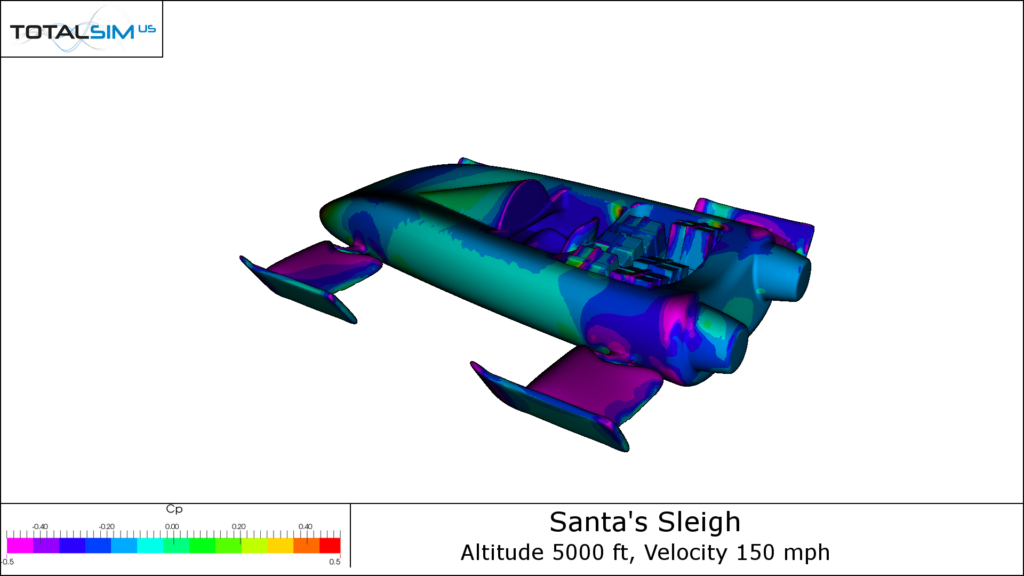
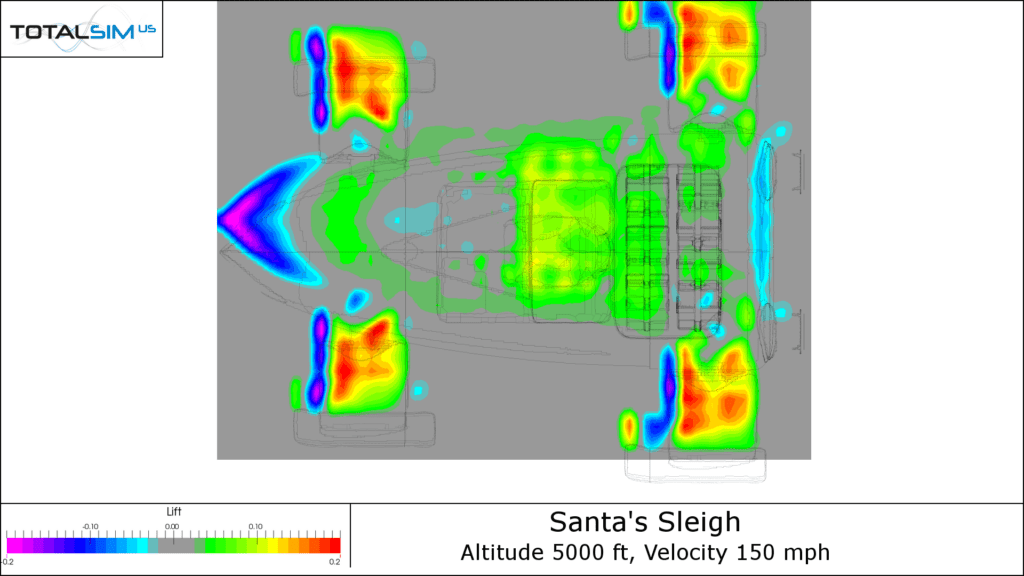
Lift X-Ray
This frog-like image is an Lift XRay plot – it shows a top view of the Jingle Jet depicting where lift is created on the sleigh. From the above plot, we can see lift created at the body as well as the skis. Negative lift is created at the nose consistent with the CpZ plots we saw above. The region of downforce on the nose coupled with the general lift of the rest of the body implies that the Jingle Jet has a very nose down pitching moment even in a standard cruise condition.
Some Christmas Math
Consider the Aerodynamic lift created on the Jingle Jet at this flying condition is 802 pounds of Lift a pretty decent amount. In order to maintain steady level flight, the 802 pounds of lift would need to be equal to the combined weight of the vehicle + its payload.
Now, let’s calculate the amount of weight expected to carry all the presents in one go. At roughly 2 billion people under the age of 18, only about 15% of them(300 Million kids) are part of cultures that expect deliveries from Santa. Of those children, assuming an equal distribution between the ages of 18, mostly the kids between 2 – 12 request Christmas presents from Santa, putting the total to 167 Million. Counting out a 20% reduction of kids on the naughty list and a subsequent 5% who request intangible gifts, Santa has to haul a payload fit for 126 Million children.
Suppose Santa’s production house hit a snafu this past year and each child is only getting a single lego block for Christmas. At an average weight of 1.152g/lego block, Santa’s payload comes to a whopping 321,700 lbs. For a more generous estimate, if each child gets a 200-piece set, then poor Santa needs to haul 64.3 Million pounds this Christmas.
As a comparison, an Airbus A380 can carry a payload of roughly 380,000 lbs. At 1 lego block per child, Santa could get the job done with an A380, but certainly not the Jingle Jet in its current form. If the Jingle Jet were scaled up to the size of an A380, the lift produced by the Jet could easily carry the payload, but that would be neglecting the weight of the Jet itself, power required, and fuel… Oh man, the aircraft designers conundrum!
Concluding Remarks
A quick CFD analysis of the Jingle Jet demonstrates where the aerodynamic lift and drag are coming from on the body of the vehicle. Some quick math shows that Santa has a gargantuan tasks ahead of him later this month and that the Jingle Jet would need some re-thinking to carry all the kids’ presents in a single delivery run. Of course this is mostly inside the box thinking… We all know Santa has a few tricks up his sleeve get the job done.
About TotalSim
Founded in 2009, TotalSim US is a full-service computational fluid dynamics (CFD) consulting and solutions group providing decades of engineering expertise and insight to top organizations in the automotive, racing, aerospace and industrial industries. TotalSim is headquartered in Dublin, Ohio, with an additional office in Pasadena, California. Together with our sister company, TotalSim UK in Brackley, England we are able to serve clients’ global needs.
What we do
We use cutting-edge technology to help you solve your most complex engineering problems. With decades of experience in aerodynamics and design, our goal is to assist you in taking your ideas from initial concept to high performance reality.
In addition to CFD consulting and custom software, we offer industry-specific applications, training, support and hardware to ensure your product is performance-ready.
What makes us different?
We are a relationship-driven company that:
- Accelerates every stage of design and development through automated CFD calculations and workflows.
- Simplifies complex CFD processes to empower our clients’ success.
- Empowers clients at every stage with solver-agnostic solutions, support and training.
- Customizes CFD tools and provides simulation apps tailored to automotive, truck and aerospace designs.
Credits
[1] Photo retrieved from Mikael Sedlacek
[2] Vehicle drawn by Mikael Sedlacek
[3] Typical Cd values retrieved from https://en.wikipedia.org/wiki/Drag_coefficient
[4] Typical L/D ratios retrieved from https://en.wikipedia.org/wiki/Lift-to-drag_ratio